直方图均衡化
基本原理
直方图均衡化,把直方图均匀的平摊开,不改变某个灰度级像素的个数。 要找到一个灰度映射函数,完成灰度映射。
直方图均衡化中,用累计直方图做了灰度映射的函数。步骤如下:
- 计算直方图
- 对直方图进行积分后,可得到累计直方图。
- 再归一化到 [0, 255] 空间,得到灰度映射函数。
- 做灰度映射。
所以每个图像都有不同的映射函数,他是动态计算的。 累计直方图是单调递增的,不会出现两个灰度级映射到同一个灰度的情况。
均衡化对偏暗或者偏亮,就是灰度级聚集在一起的地方,进行拉开,明暗分明。
代码
image1 = imread('Fig3.10(b).jpg');
figure();
subplot(2,2,1);
imshow(image1); title('原图');
subplot(2,2,2);
imhist(image1); title('原图直方图');
image2 = histeq(image1);
subplot(2,2,3);
imshow(image2); title('均衡化后');
subplot(2,2,4);
imhist(image2); title('均衡化后直方图');
结果分析
运行结果:
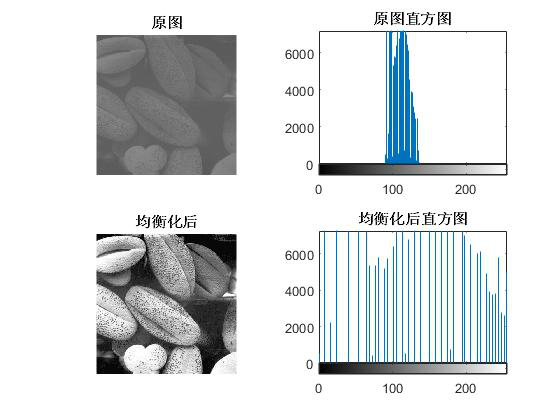
分析:
直方图均衡化是比较好能实现提高图像对比度的方法。
均衡化后的图像明暗对比更明显。亮的地方更亮,暗的地方更暗,拉开了差距。
-
增大图像的信息量。
-
直方图被均匀分开。
空域图像增强
基本原理
空域图像增强,常见的有非线性的中值滤波和高斯平滑滤波。
中值滤波的基本原理是把数字图像或数字序列中一点的值用该点的一个邻域中各点值的中值代替,让周围的像素值接近的真实值,从而消除孤立的噪声点。
高斯滤波器是一种线性滤波器,能够有效的抑制噪声,平滑图像。其作用原理和均值滤波器类似,都是取滤波器窗口内的像素的均值作为输出。其窗口模板的系数和均值滤波器不同,均值滤波器的模板系数都是相同的为1;而高斯滤波器的模板系数,则随着距离模板中心的增大而系数减小。所以,高斯滤波器相比于均值滤波器对图像个模糊程度较小。
代码
image1 = imread('Fig3.37(a).jpg');
w = fspecial('gaussian');
image2 = imfilter(image1,w);
image3 = medfilt2(image1);
subplot(1,3,1);
imshow(image1); title('原图');
subplot(1,3,2);
imshow(image2); title('高斯平滑滤波');
subplot(1,3,3);
imshow(image3); title('中值滤波');
结果分析
运行结果:

分析:
图像的噪声是椒盐噪声,在处理椒盐噪声的时候,中值滤波的效果会比高斯平滑滤波的效果更好的多。
图像锐化
基本原理
图像锐化处理的作用是使灰度反差增强,从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算,因此可以对图像进行逆运算,如微分运算能够突出图像细节,使图像变得更为清晰。由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加而产生锐化图像。
这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果,同时又能保留背景信息,将原始图像叠加到拉普拉斯变换的处理结果中去,可以使图像中的各灰度值得到保留,使灰度突变处的对比度得到增强,最终结果是在保留图像背景的前提下,突现出图像中小的细节信息。
代码
w1 = fspecial('laplacian',0);
w2 = [1 1 1;1 -8 1;1 1 1];
image1 = imread('Fig3.40(a).jpg');
image1_d = im2double(image1);
image1_f1 = imfilter(image1_d, w1, 'replicate');
image1_f2 = imfilter(image1_d, w2, 'replicate');
figure();
subplot(1,3,1);
imshow(image1); title('Fig3.40(a).jpg');
subplot(1,3,2);
imshow(image1_d-image1_f1); title('不包含对角线邻域');
subplot(1,3,3);
imshow(image1_d-image1_f2); title('包含对角线邻域');
image2 = imread('Fig10.10(a).jpg');
image2_d = im2double(image2);
image2_f1 = imfilter(image2_d, w1, 'replicate');
image2_f2 = imfilter(image2_d, w2, 'replicate');
figure();
subplot(1,3,1);
imshow(image2); title('Fig3.40(a).jpg');
subplot(1,3,2);
imshow(image2_d-image2_f1); title('不包含对角线邻域');
subplot(1,3,3);
imshow(image2_d-image2_f2); title('包含对角线邻域');
结果分析
运行结果:
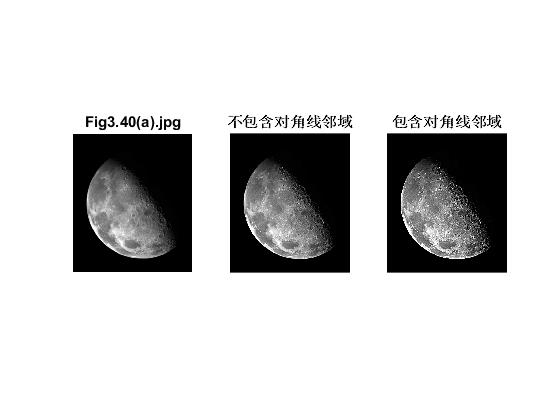
分析:
包括对角线邻域的laplacian算子增强效果会比不包括对角线邻域的laplacian算子增强效果更好,但是也会存在锐化过度的现象。包含对角分量的模板产生更锐化的效果。